إجابات الرياضيات المقترحة لامتحان القبول للصف العاشر في هانوي عام 2025

أعلنت وزارة التعليم والتدريب في هانوي عن أسئلة نموذجية لسبع مواد لامتحان القبول للصف العاشر في عام 2025. وتشمل هذه المواد السبع الأدب والرياضيات واللغات الأجنبية والعلوم الطبيعية والتاريخ والجغرافيا والتربية المدنية وتكنولوجيا المعلومات.

امتحان رياضيات توضيحي لامتحان القبول للصف العاشر في العام الدراسي 2025 في هانوي (لقطة شاشة).

بالنسبة للرياضيات، تتكون معرفة الامتحان من 3 أجزاء: الأرقام والجبر تمثل 4.5 نقطة، والهندسة والقياس تمثل 4 نقاط، والإحصاء والاحتمالات تمثل 1.5 نقطة.

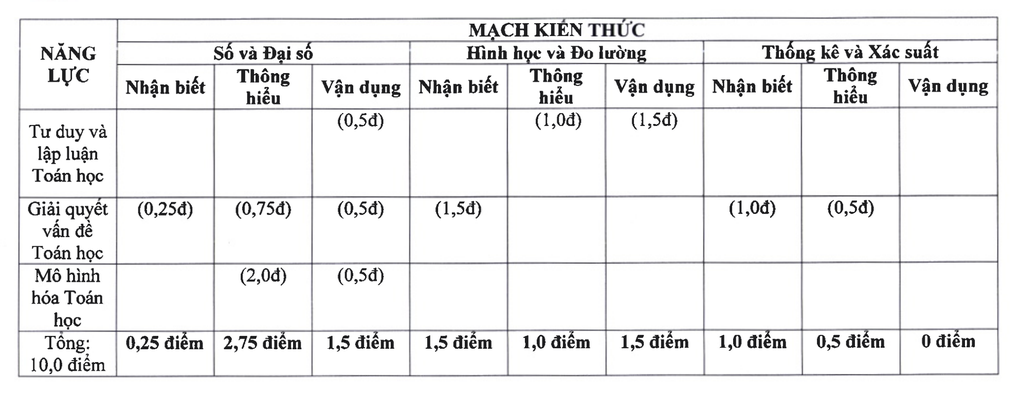
دائرة المعرفة الرياضية لامتحان القبول للصف العاشر في هانوي في عام 2025 (لقطة شاشة).

>> شاهد الإجابات المقترحة التفصيلية لامتحان الرياضيات للصف العاشر العام في هانوي في عام 2025 من معلمي القسم المهني tuyensinh247 هنا

مراجعة اختبار التوضيح في الرياضيات

وفقًا للمعلم دو فان باو، يتم ترتيب الهيكل العام للامتحان على النحو التالي:

الجزء الأول: (1.5 نقطة) يتضمن سؤالين حول الإحصاء والاحتمالات.

- إحصائيات البيانات والرسوم البيانية

- الاحتمالية

الجزء الثاني: (1.5 نقطة) يتضمن 3 أسئلة حول التعبيرات الجبرية، مشابهة للسؤال الأول في امتحانات السنوات السابقة.

- حساب قيم التعبيرات، واختبار المهارات الأساسية للطلاب

- تبسيط التعبير

- أسئلة إضافية للتمييز بين الطلاب

الدرس الثالث: (2.5 نقطة) يتضمن 3 أسئلة تتعلق بأنظمة المعادلات والمعادلات التربيعية.

- الجملة 1، 2: حل المشكلات الحياتية من خلال إنشاء نظام من المعادلات، وإنشاء المعادلات

- السؤال 3 المعادلة التربيعية

الدرس الرابع: الهندسة

- الهندسة المكانية

- مسائل حول الدوائر

الدرس الخامس. مسائل متقدمة في المتطرفات الهندسية المتعلقة بعوامل العالم الحقيقي.

المجموع الكلي: 10 نقاط، موزعة بالتساوي بين أقسام المعرفة الأساسية والمتقدمة، من الجبر والهندسة إلى التطبيقات العملية.

تعليقات على محتوى المعرفة

قسم الجبر: يتضمن محتوى أساسيًا، مثل العمليات الحسابية باستخدام التعبيرات، والمعادلات التربيعية، وتطبيقاتها. ومن مميزات هذا الاختبار التجريبي كثرة الأسئلة التي تتناول مسائل حياتية، مما يساعد الطلاب على حل مشكلاتهم الحياتية من خلال الرياضيات.

قسم الهندسة: يتضمن محتوى مألوفًا، مثل الهندسة المستوية، ومسائل الدوائر والأشكال الرباعية المحفورة، والهندسة المكانية، والبراهين الهندسية، والتطبيقات الهندسية العملية. يشترط الامتحان امتلاك الطلاب لمهارات التفكير المكاني والقدرة على تطبيق النظريات الهندسية في المسائل العملية.

قسم الإحصاء والاحتمالات: هو محتوى جديد مقارنة بامتحانات السنوات السابقة، ويظهر في الدرس الأول، ويطلب من الطلاب تحليل الرسوم البيانية وحساب الاحتمالات، وهو محتوى ذو تطبيق عملي ويظهر بشكل متكرر في برامج الكتب المدرسية الجديدة.

تعليقات على الصعوبة

المستوى الأساسي والمتوسط: أسئلة تقييم التعابير، وحل المعادلات التربيعية، وحساب الاحتمالات، جميعها في المستوى الأساسي والمتوسط. يكفي أن يكون لدى الطلاب إلمام جيد بالأساسيات ليتمكنوا من حل هذه الأسئلة.

المستوى المتقدم: تتطلب أسئلة البراهين الهندسية، والمسائل العملية المتعلقة بالهندسة المكانية، وحسابات الفائدة المصرفية من الطلاب امتلاك تفكير منطقي جيد وقدرة على تطبيق المعرفة عمليًا. غالبًا ما تُشكل هذه الأسئلة تحديًا للطلاب ذوي القدرة التعليمية المتوسطة.

تم تصميم نموذج امتحان هانوي لمتابعة برنامج التعليم العام الجديد عن كثب، مع التركيز على اختبار معارف ومهارات الطلاب بشكل شامل، وخاصة قدرتهم على تطبيقها في الممارسة العملية.

ويحتفظ الامتحان بنحو 60-70% من البنية التقليدية لكنه يتضمن ابتكارات في المحتوى وطرق صياغة الأسئلة، مما يساعد على تقييم الطلاب بشكل أكثر شمولاً.

صعوبة الامتحان متوسطة، مع وجود تمييز واضح لاختيار الطلاب الجيدين.

في السنوات السابقة، كان الامتحان غالبًا ما يُميّز بوضوح بين الطلاب الجيدين والمتوسطين من خلال أسئلة الجبر والهندسة البحتة. أما الامتحان النموذجي، فقد أضاف عناصر عملية، مُلزمًا الطلاب ليس فقط بالمعرفة، بل أيضًا بفهم كيفية تطبيقها في مواقف مُحددة.

شهد هيكل الامتحان التوضيحي هذا العام تطورًا ملحوظًا مقارنةً بالأعوام السابقة، حيث تم تصنيف محتوى الدروس، وتداخل أنواع الأسئلة، وزيادة في عدد المسائل العملية. يعكس هذا توجه البرنامج التعليمي الجديد، الذي يركز بشكل أكبر على اختبار قدرة الطلاب على تطبيق المعرفة والتفكير المترابط.

لتحقيق أداء جيد في الامتحان، يحتاج طلاب الصف التاسع إلى:

للاستعداد بشكل جيد لامتحان القبول للصف العاشر بنفس هيكل ومحتوى الامتحان النموذجي، يحتاج طلاب الصف التاسع إلى اتباع الخطوات التالية:

1. فهم الأساسيات

الجبر: يجب إتقان المعرفة الأساسية في برنامج الصف التاسع، بما في ذلك:

المعادلات من الدرجة الأولى والثانية، الحلول والخصائص.

الصيغ المتعلقة بالهندسة المستوية والصلبة، وخاصة النظريات المتعلقة بالمثلثات والدوائر والأشكال الهندسية الأساسية.

حل المشكلات عن طريق إعداد المعادلات

الهندسة: المعرفة، والنظرية حول الدوائر والأشكال الرباعية المحيطية وخصائصها، وإثبات المثلثات المتشابهة وتطبيق خصائص المثلثات المتشابهة،...

الإحصاء والاحتمالات: من الضروري الإلمام بالمفاهيم الإحصائية الأساسية مثل الهستوجرامات، وجداول التكرار، وحسابات الاحتمالات البسيطة، حيث أن هذه أقسام قد تظهر في الامتحان.

2. التدرب على حل مسائل الرياضيات الحقيقية

الرياضيات التطبيقية: يحتاج الطلاب إلى التدرب على حل المشكلات المتعلقة بالحياة الواقعية، وحل المشكلات عن طريق إعداد المعادلات، وأنظمة المعادلات، ومشاكل الإنتاج والإدارة، أو المشكلات المتعلقة بالهندسة المكانية.

تطبيق المعرفة على الواقع: تمارين عملية حول قياس وحساب الحجم والمساحة. هذا يُساعد الطلاب على فهم كيفية تطبيق الرياضيات في الحياة بشكل أفضل.

3. ممارسة التفكير المنطقي والمهارات التحليلية

البرهان الرياضي: تعزيز الممارسة في مسائل البرهان الهندسي والجبري. وتحديدًا، تُعدّ المسائل التي تتطلب إثبات العلاقات بين عناصر المستوي أو الهندسة المكانية ضرورية لتحسين التفكير المنطقي.

حلل وحل المسائل: تدرب على تحليل الأسئلة وفهم متطلبات كل سؤال قبل البدء بحلها. هذا يُجنّبك الالتباس ويزيد من دقة الاختبار.

المصدر: https://dantri.com.vn/giao-duc/goi-y-dap-an-mon-toan-de-minh-hoa-thi-vao-10-cua-ha-noi-nam-2025-20240829150755869.htm